Physics-Informed Residual Adaptive Networks (PirateNets) is a neural network architecture designed to enable efficient and stable training of deep Physics-Informed Neural Networks (PINNs).
Problem:
Machine learning plays a key role in advancing science by analyzing complex data, building predictive models, and uncovering nonlinear relationships. Physics-Informed Machine Learning (PIML) incorporates physical laws and constraints into models, with PINNs as a key example. PINNs use tailored loss functions that bias the models to adhere to physical principles during training, showing promise across computational science. However, challenges such as spectral bias, unbalanced back-propagated gradients, causality violation, and initialization pathologies limit their performance, especially in deeper architectures. While progress has been made, most PINNs still rely on shallow networks, underutilizing the full potential of deep networks.
Solution:
PirateNets is a neural network architecture designed for stable and efficient training of deep PINNs. Unlike existing methods, PirateNets overcome initialization challenges, scale effectively to deeper networks, and integrate physical priors for improved robustness. This approach offers improved accuracy, scalability, and stability compared to traditional PINNs and alternative architecture.
Technology:
PirateNets addresses the problem of pathological initialization in PINNs, enabling stable and efficient scaling for implementing deep networks. Architecture leverages adaptive residual connections with trainable parameters that allow the networks to begin as shallow networks that progressively deepen during training. This approach ensures the network is initially represented as a linear combination of a chosen basis, effectively addressing initialization challenges and facilitating the integration of physical priors during model setup.
Advantages:
- Enhances the approximation capacity, trainability, and robustness of the deep learning neural network model
- Improved flexibility in integrating physical priors
- Outperforms the current state-of-the-art approach with a substantially lower Relative L² error (4.27 X 10¯⁴ vs 2.45 X 10¯³) when exploring a one-dimensional Korteweg De Vries (KdV) equation, a model used to describe the dynamics of solitary waves
- Outperforms the accuracy achieved by the Modified Multi-layer Perceptron (MLP) backbone when solving a scalar PDE involving a complex variable (Ex. Ginzburg-Landau equation in 2D, where the computed L² error for the real and imaginary part are 1.49 X 10¯² and 1.90 X 10¯², respectively, compared to 3.2 X 10¯² and 1.94 X 10¯² achieved by the MLP)
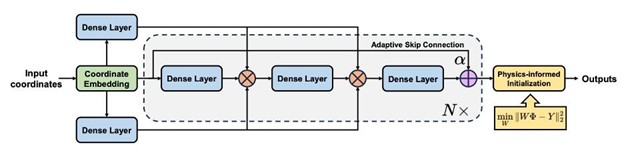
This figure illustrates the architecture of PirateNets. Input coordinates are mapped into a high-dimensional feature space using random Fourier features and passed through N adaptive residual blocks, each containing three dense layers with gating operations. Adaptive skip connection (á) ensures identity mapping at initialization, avoiding pathological initialization. The final layer uses physics-informed initialization, and the model progressively deepens as training activates nonlinearities.
Case ID:
24-10783-TpNCS
Web Published:
11/25/2025
Patent Information:
| App Type |
Country |
Serial No. |
Patent No. |
File Date |
Issued Date |
Expire Date |